We should forget about small efficiencies, say about 97% of the time: premature optimization is the root of all evil. Yet we should not pass up our opportunities in that critical 3%.
Measure. Don't tune for speed until you've measured, and even then don't unless one part of the code overwhelms the rest.
We spend a lot of our time in the modern, web services-driven technology industry ignoring performance issues. What's the point of micro-optimizing a 3ms function call when each request spends 8 or 9 seconds inside the SQLAlchemy ORM? Well, sometimes it's nice to practice those optimizion skills anyway, and today I'm going to walk you through micro-optimizing a simple problem and we'll see just how much better we can do than a naive solution... even though we probably normally shouldn't.
The Problem
Our problem will be a very simple one: sum a list of n integers. To make this fair, we will assume that the integers all fit in a 32-bit signed int, and that their sum fits in a 32-bit signed int.
Of course, we're going to be micro-optimizing here, so something that warrants careful consideration is how we will measure our performance. Normally, one would use wall-time (measured with something like the Python timeit module. However, just calling time.clock() in python costs about 30 microseconds! Oh, that isn't very impressive. Let me rephrase: calling time.clock() in python costs about 60,000 cycles on a modern CPU. Instead, I propose that we directly count CPU cycles. There are some issues with this (particularly if frequency scaling is enabled, or if you have multiple cores and your OS's scheduler likes rescheduling things), but it's by far the most accurate, lowest-overhead metric of CPU performance we can get. On Intel x86, this is implemented with the RDTSC instruction (even more specifically: the serializing RDTSCP instruction)1. I've wrapped this in a Python library for easy consumption.
Here's my specific test plan:
- I will create a data-file containing n randomly generated integers in the range (0, 212). These will be randomly-generated with a fixed seed.
- For each test case, we will first load this data.
- For each test case, we will measure the cycles elapsed using the
RDTSCinstruction - We will repeat each test case at least 100 times.
All tests in this document were carried out on my 2013 15" rMBP with its Intel Core i7-4850HQ. I also ran them on my work laptop, a 2014 13" rMBP with Intel Core i5-4308U to ensure that the results were sane.
First Attempts: Python
I like Python. It's a friendly, duck-typed language with many of the convenient features of object oriented and functional programming languages. Loading the data in from a file is easy:
import array
data = array.array("i")
with open(sys.argv[1], "r") as f:
for line in f:
data.append(int(line.strip()))
Here's the most naive possible solution to this problem:
def sum_naive_python():
result = 0
for i in data:
result += i
return result
Look how obvious that code is! Beautiful! This code takes 50,000,000 ± 3% cycles to run on my machine. That is about 24ms. However, I'm not really interested in the absolute amount of time — I'm interested in how it scales. So the metric I'm going to use is the number of points summed per cycle. In an ideal single-issue non-superscalar CPU with perfect branch prediction, we'd expect to do 1.0 points per cycle. On that metric, this first shot is awful: 0.01 points per cycle. Here's how it scales as a function of the number of points:
There's a straightforward improvement here — Python includes a native sum function which is implemented in C and should be way faster. Here's our next test function:
def sum_native_python():
return sum(data)
This one does a good deal better: 12,000,000 ± 2% cycles, 0.04 points per cycle. Still pretty awful, but four times faster!
What if we tried to use a fancy numeric library for Python? How about numpy? That calls out into optimized FORTRAN code, so it ought to be super-fast!
Nope! It looks like NumPy's overhead kills us — we only get 0.004 points per cycle here (one tenth of the native sum function over the built-in array type).
Moving on Up: C
It's a common pattern in Python that when you can't make it any faster in Python, you switch to C. So let's do that. I've got an equivalent test rig set up for C which reads the file into a heap-allocated array of ints (I won't bother showing it here because it's quite long), and here's our first attempt at a C function to sum these dang numbers:
int sum_simple(int* vec, size_t vecsize)
{
int res = 0;
for (int i = 0; i < vecsize; ++i) {
res += vec[i];
}
return res;
}
This is pretty much as elegant as the original Python code. How does it perform?
3,423,072 cycles (~1.5ms). 0.162 points per cycle. This is a 10x speedup over Python.
Note: compiled using Apple LLVM 6.0 / clang-600.0.56 with -O0
Can we do better?
I remember hearing once that unrolling loops was the solution to high performance. When you unroll a loop, you're hiding the overhead of the jump at the end of the loop and doing the branch predictor's job for it. Here's a four-way unrolled version:
int sum_unroll_4(int* vec, size_t vecsize)
{
int res = 0;
int i;
for (i = 0; i < vecsize - 3; i+=4) {
res += vec[i];
res += vec[i+1];
res += vec[i+2];
res += vec[i+3];
}
for (; i < vecsize; ++i) {
res += vec[i];
}
return res;
}
How do unrolled loops perform? Pretty much the same (0.190 points per cycle)
Maybe we just aren't unrolling enough? Well, here's an 8-way loop unroll:
int sum_unroll_8(int* vec, size_t vecsize)
{
int res = 0;
int i;
for (i = 0; i < vecsize; i+=8) {
res += vec[i];
res += vec[i+1];
res += vec[i+2];
res += vec[i+3];
res += vec[i+4];
res += vec[i+5];
res += vec[i+6];
res += vec[i+7];
}
for (; i < vecsize; ++i) {
res += vec[i];
}
return res;
}
Meh. 0.192 PPC.
Fun fact: the branch predictors on modern processors are really, really good. Unrolling loops will help for very short loops, or loops where the branch predictor for some reason is catastrophically bad, but it's almost never worth your time.
Optimizing Compilers
Those of you who have written C before have probably been wondering something here. Why am I compiling with -O0? Modern compilers have decades of optimizations programmed into them and can probably outperform anything I can write, right?
You're absolutely right! At -O3, the generated code absolute smokes everything else, with 4.462 points per cycle!
Wait... More than one point per cycle? How is that possible?
Now, dear readers, we have to take a brief digression into the land of processors.
Multi-Issue, Super-Scalar, Out-of-Order Vector Processing Machines
Once upon a time, computer processors were fairly simple. They consumed an instruction at a time, took one or more cycles to process it, then put out a result.
That ended in 1965 with the release of the Cray 6600 and ended on the desktop in 1995 with the release of the P6 Pentium Pro, both of which are examples of superscalar architectures.
Roughly speaking, a superscalar architecture includes multiple execution units (which are often specialized: maybe you'll have two general purpose arithmetic units, a couple of address calculation units, a SIMD unit, a FPU, etc) and can dispatch multiple instructions to execute in parallel on different execution units.
On an Intel Haswell CPU like mine, the architecture looks like the following2
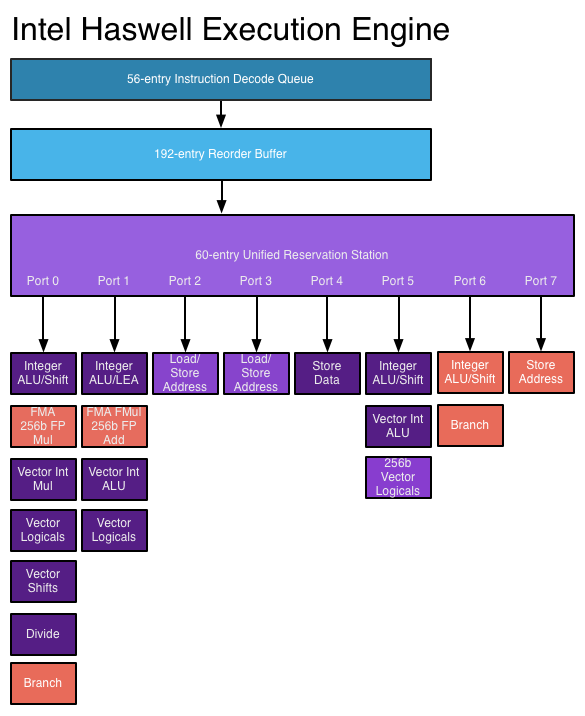
This means that we can have multiple instructions going at once, so our previous maximum of 1.0 adds per cycle is far too low.
The last piece of the puzzle is the mysterious acronym SIMD (Single Instruction, Multiple Data). SIMD instructions, also known as vector instructions apply arithmetic functions to multiple pieces of data at once. With Intel's SSE unit, for example, you can apply functions to four 32-bit integers at once, or two 64-bit floating-point numbers.
There have been a bunch of SIMD units in X86, starting with the MMX extensions, then SSE, SSE2, SSE3, SSE4.1, AVX, AVX2, and the forthcoming-but-not-yet-released AVX-512. I won't go into the technical details, but they're all in1 if you want to know more.
On a Haswell processor, which has two "Vector Int ALU"s, you can theoretically be doing two AVX2 operations in parallel, each of which can be operating on eight 32-bit integers at once. According to the Intel 64 and IA32 Architectures Optimization Reference Manual, each of these instructions has a latency of 1 cycle, giving us a maximum theoretical PPC of 16.0, which is quite a lot. In fact, it's impossibly much. Transferring 16 32-bit words to the CPU per cycle would require 64 bytes/cycle of memory throughput, which translates on my CPU to 147GB/s of memory throughput. The PC3-12800 RAM in my system can do a maximum of 12.8GB/s per stick (25.6GBps total), which is only 11 bytes per cycle. That gives us a maximum throughput from memory of slightly above 2.75 PPC. Anything above that is probably an artifact of the lovely 128MB of eDRAM L4 cache on my CPU.
Beating the Compiler
So, can we best the compiler? Can we outperform 4.462 PPC? Obviously not in the long run, but as long as our data stays small enough to fit in the high-bandwidth L3 and L4 caches, sort of. Here's my simplest winning submission, with a PPC of 4.808:
int sum_avx2_unroll4(int* vec, size_t vecsize)
{
unsigned int vec_out[8] __attribute__ ((aligned(64)));
size_t processed = 0;
asm(
"XORQ %%rax,%%rax\n\t"
"VPXOR %%ymm0,%%ymm0,%%ymm0\n\t"
"VPXOR %%ymm5,%%ymm5,%%ymm5\n\t"
"VPXOR %%ymm6,%%ymm6,%%ymm6\n\t"
"VPXOR %%ymm7,%%ymm7,%%ymm7\n\t"
"VPXOR %%ymm8,%%ymm8,%%ymm8\n\t"
"top%=:\n\t"
"VMOVDQA (%1, %%rax, 4),%%ymm1\n\t"
"VMOVDQA 32(%1, %%rax, 4),%%ymm2\n\t"
"VMOVDQA 64(%1, %%rax, 4),%%ymm3\n\t"
"VMOVDQA 96(%1, %%rax, 4),%%ymm4\n\t"
"ADDQ $32,%%rax\n\t"
"VPADDD %%ymm1,%%ymm5,%%ymm5\n\t"
"VPADDD %%ymm2,%%ymm6,%%ymm6\n\t"
"VPADDD %%ymm3,%%ymm7,%%ymm7\n\t"
"VPADDD %%ymm4,%%ymm8,%%ymm8\n\t"
"CMP %2,%%rax\n\t"
"JL top%=\n\t"
"VPADDD %%ymm5,%%ymm0,%%ymm0\n\t"
"VPADDD %%ymm6,%%ymm0,%%ymm0\n\t"
"VPADDD %%ymm7,%%ymm0,%%ymm0\n\t"
"VPADDD %%ymm8,%%ymm0,%%ymm0\n\t"
"VMOVDQA %%ymm0, 0(%3)\n\t"
"MOVQ %%rax, %0\n\t"
: "=r"(processed)
: "r"(vec), "r"(vecsize), "r"(vec_out)
: "rax", "ymm0", "ymm1", "ymm2", "ymm3", "ymm4", "ymm5", "ymm6", "ymm7", "ymm8", "cc"
);
int res = 0;
for (int i = 0; i < 8 ; ++i) {
res += vec_out[i];
}
for (; processed < vecsize; ++processed) {
res += vec[processed];
}
return res;
}
This is a four-way unroll of an AVX2-based vectorized version. It also sums into independent accumulator registers to slightly improve IPC.
Graph:
Does it really beat the compiler, though? Here's the two PPC's side by side:
Technically, mine never loses. For your edification, here's the assembly that the compiler generates:
## BB#2: ## %vector.body.preheader
pxor %xmm0, %xmm0
xorl %ecx, %ecx
pxor %xmm1, %xmm1
.align 4, 0x90
LBB8_3: ## %vector.body
## =>This Inner Loop Header: Depth=1
movdqa %xmm1, %xmm2
movdqa %xmm0, %xmm3
movdqu (%rdi,%rcx,4), %xmm0
movdqu 16(%rdi,%rcx,4), %xmm1
paddd %xmm3, %xmm0
paddd %xmm2, %xmm1
addq $8, %rcx
cmpq %rcx, %rax
jne LBB8_3
## BB#4:
movq %rax, %rcx
LBB8_5: ## %middle.block
paddd %xmm1, %xmm0
movdqa %xmm0, %xmm1
movhlps %xmm1, %xmm1 ## xmm1 = xmm1[1,1]
paddd %xmm0, %xmm1
phaddd %xmm1, %xmm1
movd %xmm1, %eax
cmpq %rsi, %rcx
je LBB8_8
## BB#6: ## %.lr.ph.preheader13
leaq (%rdi,%rcx,4), %rdx
subq %rcx, %rsi
.align 4, 0x90
LBB8_7: ## %.lr.ph
## =>This Inner Loop Header: Depth=1
addl (%rdx), %eax
addq $4, %rdx
decq %rsi
jne LBB8_7
The compiler decided to do a 2-way unrolling into SSE2 registers. Snazzy!
Conclusions
Python (like most other dynamically-typed languages) may be "fast enough", but nobody'll ever accuse it of being fast. You can get a lot of going to a low-level language like C, and you can get even slightly more by writing your own assembly, but you should probably just trust the compiler. However, if you have to sum a bunch of 12-bit numbers really quickly, well, here's your answer for you:
| Algorithm | Cycles for 500k Points | Points per Cycle |
|---|---|---|
| sum_numpy | 110681288 ± 0% Cycles | 0.005 ± 0% PPC |
| sum_naive_python | 48255863 ± 1% Cycles | 0.010 ± 1% PPC |
| sum_native_python | 12063768 ± 2% Cycles | 0.041 ± 2% PPC |
| -O0 simple | 3095247 ± 1% Cycles | 0.162 ± 1% PPC |
| -O2 simple | 2889994 ± 1% Cycles | 0.173 ± 1% PPC |
| -O0 unroll_4 | 2630305 ± 2% Cycles | 0.190 ± 2% PPC |
| -O0 unroll_8 | 2597596 ± 0% Cycles | 0.192 ± 0% PPC |
| -O2 unroll_8 | 2461759 ± 1% Cycles | 0.203 ± 1% PPC |
| -O2 unroll_4 | 2419625 ± 1% Cycles | 0.207 ± 1% PPC |
| -O2 unroll_4_asscom | 1134117 ± 1% Cycles | 0.441 ± 1% PPC |
| -O0 unroll_4_asscom | 1091086 ± 2% Cycles | 0.458 ± 2% PPC |
| -O3 unroll_4 | 393973 ± 4% Cycles | 1.269 ± 4% PPC |
| -O3 unroll_8 | 334532 ± 0% Cycles | 1.495 ± 0% PPC |
| -O0 asm_unroll_8 | 266224 ± 3% Cycles | 1.878 ± 3% PPC |
| -O3 unroll_4_asscom | 254489 ± 1% Cycles | 1.965 ± 1% PPC |
| -O2 asm_unroll_8 | 227831 ± 1% Cycles | 2.195 ± 1% PPC |
| -O3 asm_unroll_8 | 227390 ± 0% Cycles | 2.199 ± 0% PPC |
| -O0 avx2_and_scalar_unroll | 149051 ± 0% Cycles | 3.355 ± 0% PPC |
| -O3 avx2_and_scalar_unroll | 146261 ± 0% Cycles | 3.419 ± 0% PPC |
| -O2 avx2_and_scalar_unroll | 144545 ± 0% Cycles | 3.459 ± 0% PPC |
| -O3 sse2 | 125397 ± 2% Cycles | 3.987 ± 2% PPC |
| -O0 sse2 | 123398 ± 0% Cycles | 4.052 ± 0% PPC |
| -O2 sse2 | 119917 ± 0% Cycles | 4.170 ± 0% PPC |
| -O3 simple | 112045 ± 0% Cycles | 4.462 ± 0% PPC |
| -O0 avx2 | 111489 ± 0% Cycles | 4.485 ± 0% PPC |
| -O2 avx2 | 110661 ± 0% Cycles | 4.518 ± 0% PPC |
| -O3 avx2_unroll4_mem_address | 110342 ± 0% Cycles | 4.531 ± 0% PPC |
| -O3 avx2_unroll4 | 109213 ± 1% Cycles | 4.578 ± 1% PPC |
| -O3 avx2 | 107011 ± 0% Cycles | 4.672 ± 0% PPC |
| -O2 avx2_unroll4 | 106253 ± 0% Cycles | 4.706 ± 0% PPC |
| -O2 avx2_unroll4_mem_address | 105458 ± 1% Cycles | 4.741 ± 1% PPC |
| -O0 avx2_unroll4 | 103996 ± 0% Cycles | 4.808 ± 0% PPC |
| -O0 avx2_unroll4_mem_address | 101976 ± 0% Cycles | 4.903 ± 0% PPC |
Cheers.
you should read the Intel Software Developer's Manual if you want to know more
Want to comment on this? How about we talk on Mastodon instead? Share on Mastodon
Share on Mastodon